- Binary Variables
- Multinomial Variables
- The Gaussian Distribution
- The Exponential Family
Binary Variables
Coin flipping: heads=1, tails=0 $$p(x=1|\mu) = \mu$$
Bernoulli Distribution
One coin flipping $$Bern(x|\mu) = \mu^x(1-\mu)^{1-x}$$
Bernoulli Family
来自瑞士巴塞尔的商人与学者家族
- 雅各布·伯努利(1654–1705),在概率方面的贡献突出,以伯努利分布而闻名。
- 约翰·伯努利(1667–1748),雅各布的弟弟,以最速降线而闻名,教授过欧拉。变分法开创者。把洛必达法则卖给洛必达。
- 丹尼尔·伯努利(1700–1782),约翰的小儿子,在流体力学方面贡献突出,以伯努利定律而闻名。
Probability Density Function
For discrete distributions, the pdf is also known as the probability mass function (pmf). $$ f(x | p)= \begin{cases}1-p, & x=0 \newline p, & x=1 \end{cases} $$
Cumulative Distribution Function
$$ F(x | p)= \begin{cases}1-p, & x=0 \newline p, & x=1 \end{cases} $$
Descriptive Statistics
$$ \begin{aligned} \mathbb{E}[x] &=\mu \newline \operatorname{var}[x] &=\mu(1-\mu) \end{aligned} $$
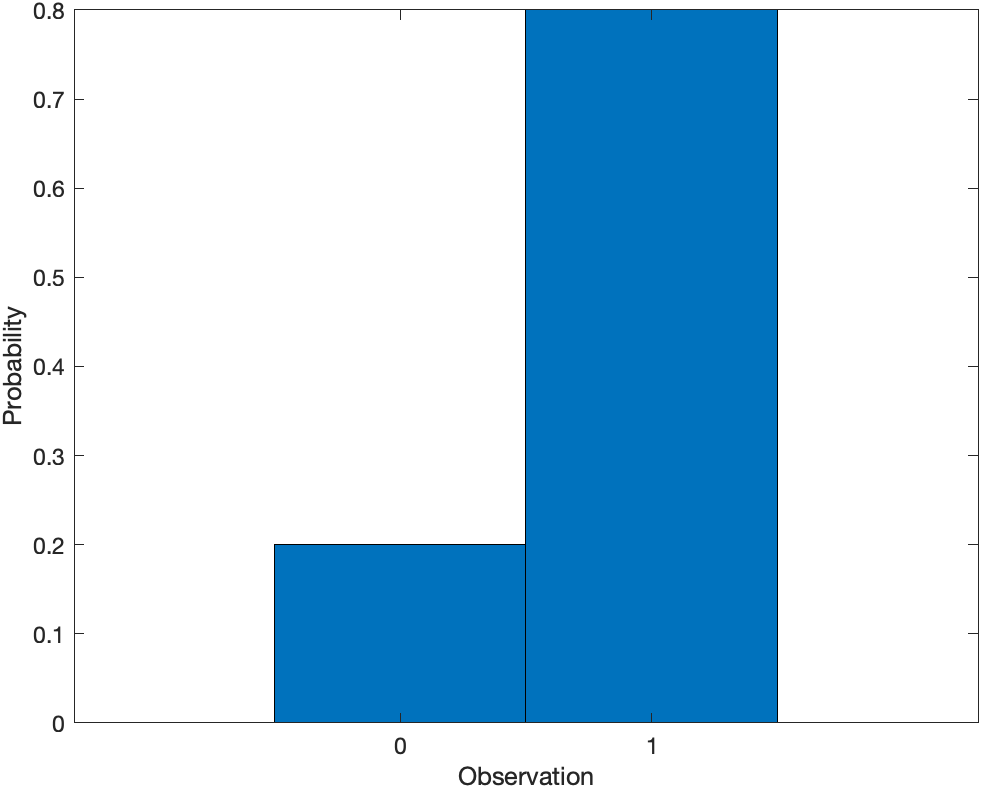
Examples
The Bernoulli distribution is a special case of the binomial distribution, where N = 1.
1p = 0.8;
2x = 0:1;
3y = binopdf(0:1,1,p);
4bar(x,y,1)
5xlabel('Observation')
6ylabel('Probability')
Binomial Distribution
N coin flips: $p(m heads|N,\mu)$
$$ \operatorname{Bin}(m \mid N, \mu)=\left(\begin{array}{l} N \newline m \end{array}\right) \mu^{m}(1-\mu)^{N-m} $$
Probability Density Function
For discrete distributions, the pdf is also known as the probability mass function (pmf). $$ f(x \mid N, p)=\left(\begin{array}{c} N \newline x \end{array}\right) p^{x}(1-p)^{N-x} \quad ; \quad x=0,1,2, \ldots, N $$
Cumulative Distribution Function
$$ F(x \mid N, p)=\sum_{i=0}^{x}\left(\begin{array}{c} N \newline i \end{array}\right) p^{i}(1-p)^{N-i} \quad ; \quad x=0,1,2, \ldots, N $$
Descriptive Statistics
$$ \begin{aligned} \mathbb{E}[m] &=N\mu \newline \operatorname{var}[m] &=N\mu(1-\mu) \end{aligned} $$
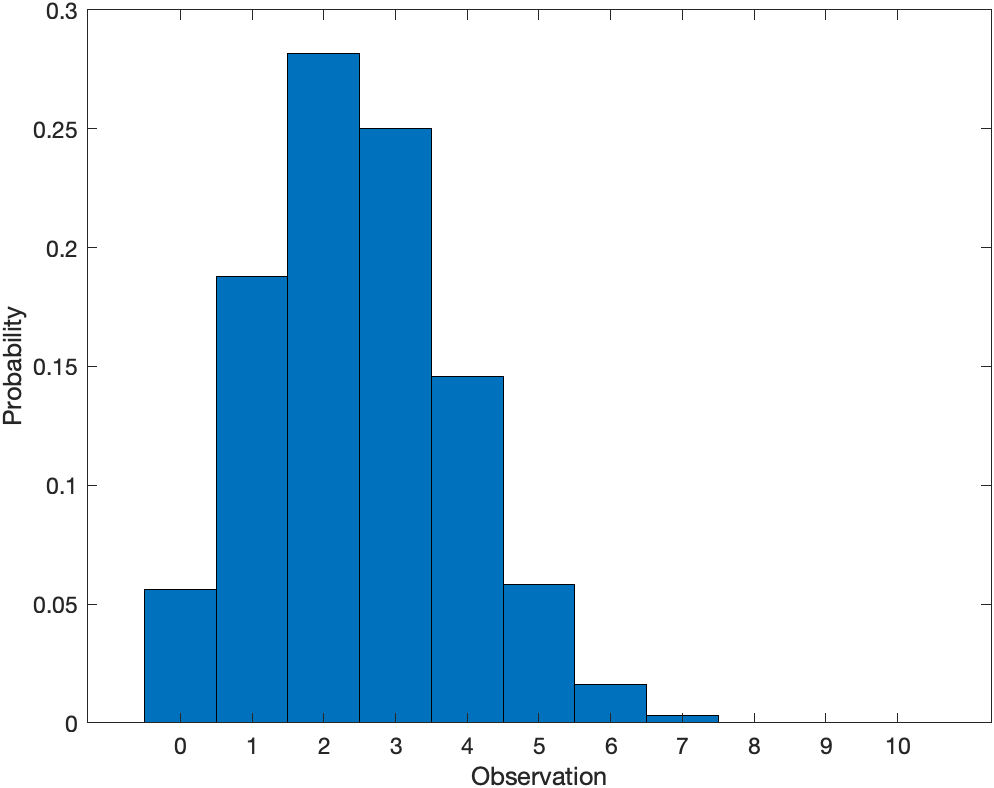
Examples
The Bernoulli distribution is a special case of the binomial distribution, where N = 1.
1x = 0:10;
2y = binopdf(x,10,0.25);
3bar(x,y,1)
4xlabel('Observation')
5ylabel('Probability')
MLE(maximum likelihood estimator) for binomial
max $\ln p(\mathcal{D}|\mu)$ The MLE is just the sample mean: $\mu_{ML} = 1/N \sum_{n=1}^{N}x_n$
Over-fitting problem
Underestimate the variance
Bayes treatment of Binary Variables
the beta distribution
$$ \operatorname{Beta}(\mu \mid a, b)=\frac{\Gamma(a+b)}{\Gamma(a) \Gamma(b)} \mu^{a-1}(1-\mu)^{b-1} $$
Gamma function is defined by
Gamma function
$$ \Gamma(z)=\int_{0}^{\infty} x^{z-1} e^{-x} d x $$ It is known as the Euler integral of the second kind.
Given that $\Gamma(1)=1$ and $\Gamma(n+1)=n \Gamma(n)$, $\Gamma(n)=1 \cdot 2 \cdot 3 \cdots(n-1)=(n-1) !$
we can use beta function here as well
Beta function
$$ \mathrm{B}(x, y)=\int_{0}^{1} t^{x-1}(1-t)^{y-1} d t $$
The beta function is also called the Euler integral of the first kind.
- It is symmetric,$B(x,y) = B(y,x)$
- It is related to Gamma function $B(x,y) =\Gamma(x)\Gamma(y)/\Gamma(x+y))$
then we can rewrite the Beta distribution with Beta function
$$ \operatorname{Beta}(\mu \mid a, b)=\frac{1}{B(x,y)} \mu^{a-1}(1-\mu)^{b-1} $$
The Beta distribution provides the conjugate prior for the Bernoulli distribution. ???
Descriptive Statistics
$$ \begin{aligned} \mathbb{E}[\mu] &=\frac{a}{a+b}\newline \operatorname{var}[\mu] &=\frac{ab}{(a+b)^2(a+b+1)} \end{aligned} $$
hyperparameters
a and b are also called hyperparameters.
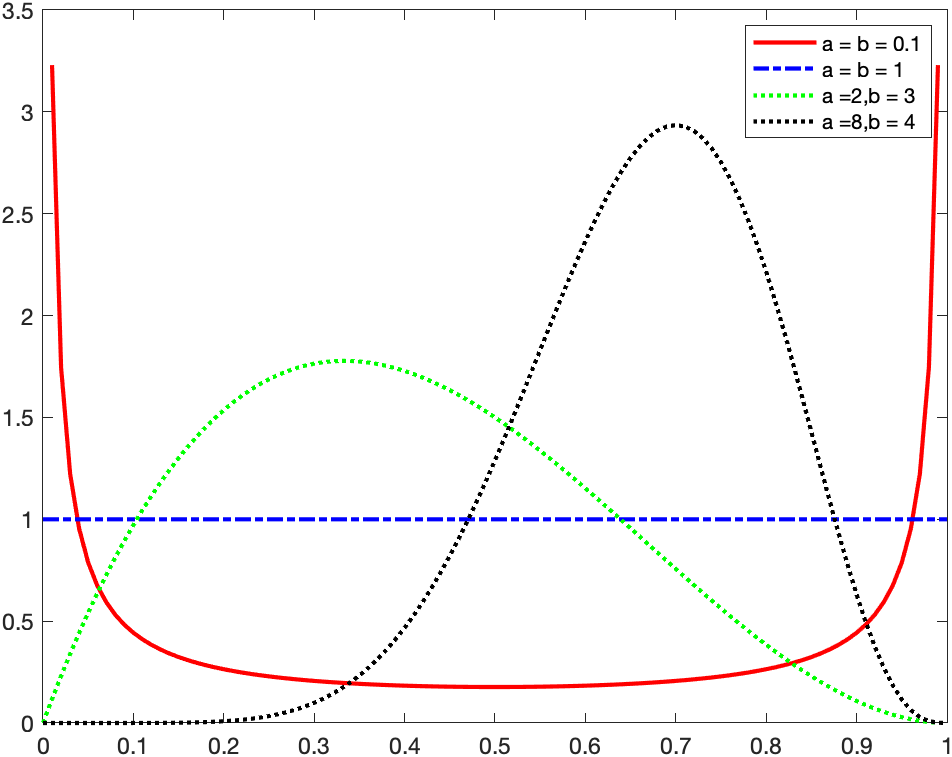
1X = 0:.01:1;
2y1 = betapdf(X,0.1,0.1);
3y2 = betapdf(X,1,1);
4y3 = betapdf(X,2,3);
5y4 = betapdf(X,8,4);
6
7figure
8plot(X,y1,'Color','r','LineWidth',2)
9hold on
10plot(X,y2,'LineStyle','-.','Color','b','LineWidth',2)
11plot(X,y3,'LineStyle',':','Color','g','LineWidth',2)
12plot(X,y4,'LineStyle',':','Color','k','LineWidth',2)
13legend({'a = b = 0.1','a = b = 1','a =2,b = 3','a =8,b = 4'},'Location','NorthEast');
14hold off
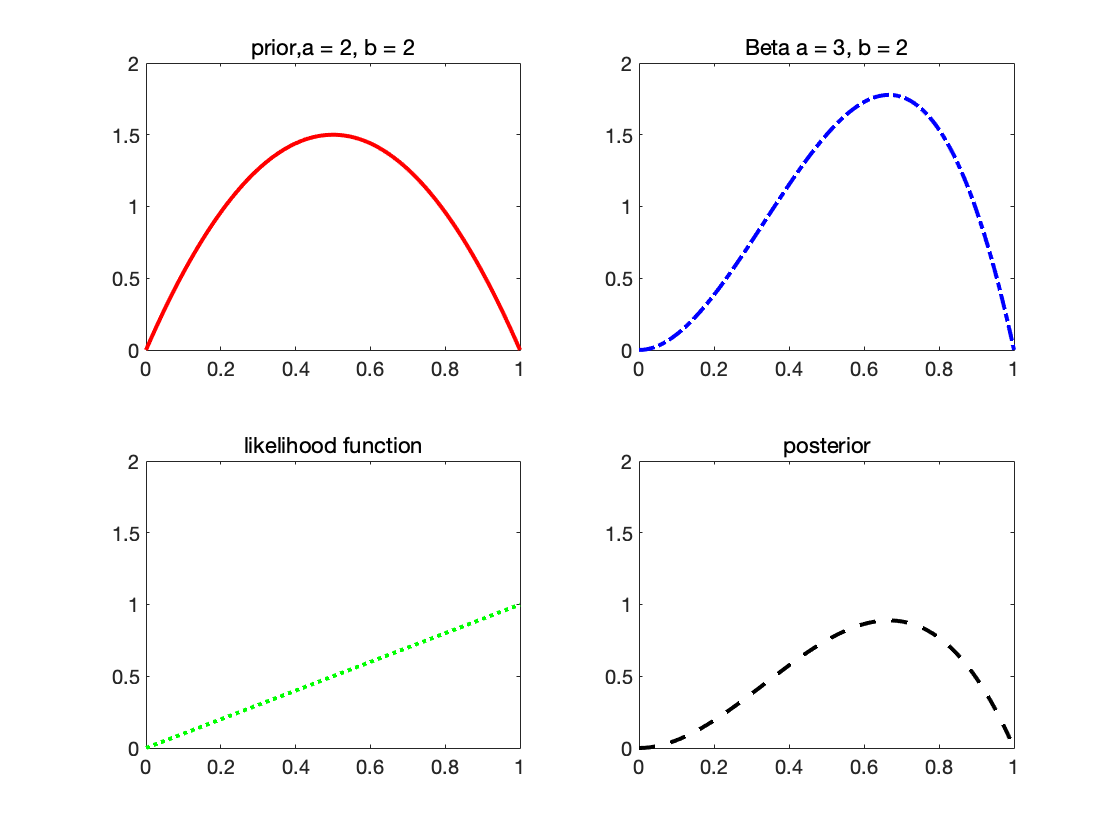
Prior·Likelihood = Posterior
Posterior =
$$ \begin{aligned} p\left(\mu \mid a_{0}, b_{0}, \mathcal{D}\right) & \propto p(\mathcal{D} \mid \mu) p\left(\mu \mid a_{0}, b_{0}\right) \newline &=\left(\prod_{n=1}^{N} \mu^{x_{n}}(1-\mu)^{1-x_{n}}\right) \operatorname{Beta}\left(\mu \mid a_{0}, b_{0}\right) \newline & \propto \mu^{m+a_{0}-1}(1-\mu)^{(N-m)+b_{0}-1} \newline & \propto \operatorname{Beta}\left(\mu \mid a_{N}, b_{N}\right) \end{aligned} $$
where $a_N = a_0 +m$, $b_N = b_0 +(N-m)$
1X = 0:.01:1;
2y1 = betapdf(X,2,2);
3y2 = betapdf(X,3,2);
4y3 = 1/1 * X;
5y4 = y1.*y3;
6
7figure
8subplot(2,2,1)
9plot(X,y1,'Color','r','LineWidth',2);title('prior,a = 2, b = 2');ylim([0,2]);
10subplot(2,2,2)
11plot(X,y2,'LineStyle','-.','Color','b','LineWidth',2);title('Beta a = 3, b = 2');ylim([0,2]);
12subplot(2,2,3)
13plot(X,y3,'LineStyle',':','Color','g','LineWidth',2);title('likelihood function');ylim([0,2]);
14subplot(2,2,4)
15plot(X,y4,'LineStyle','--','Color','k','LineWidth',2);title('posterior');ylim([0,2]);