- 线性模型、神经网络、核方法、图模型和近似推断 等机器学习方法
- 介绍蒙特卡洛、广义多项式混沌、PDF/CDF方法、数据 同化等不确定性量化方法
- 熟练掌握这些方法的数值实现和计算机建模
Uncertainty Quantification (UQ)
- 随机不确定性
- 认知不确定性
Machine Learning (ML)
- Supervised learning: classification, regression
- Unsupervised learning: clustering, density estimation, visualization
- Reinforcement learning: maximize a reward
学习路线
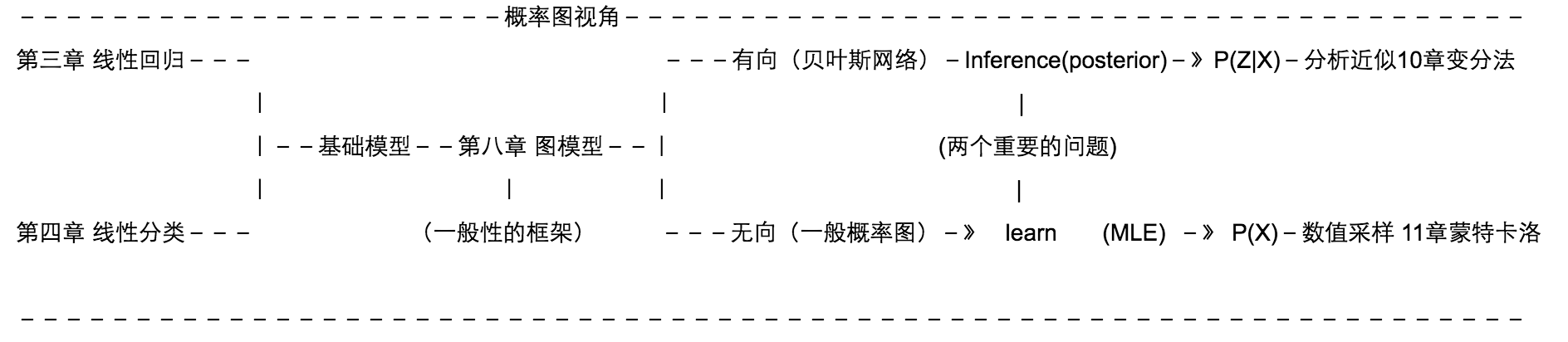
Chapter1: Introduction
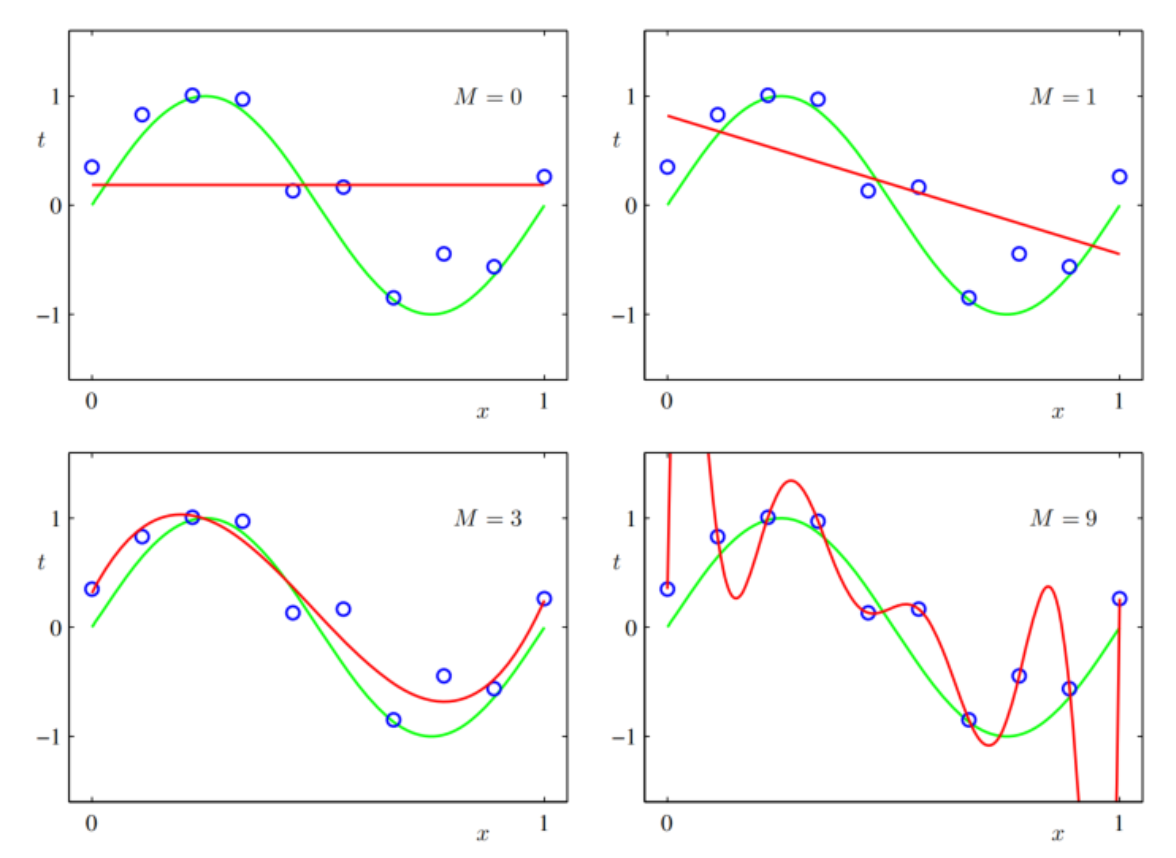
Polynomial Curve Fitting (1D)
$sin(2\pi x)$ the prepare data x is set by the correspond value of $sin(2\pi x)$ with a Gaussian distribution noise. \begin{equation} y(x, \mathbf{w})=w_{0}+w_{1} x+w_{2} x^{2}+\ldots+w_{M} x^{M}=\sum_{j=0}^{M} w_{j} x^{j} \end{equation}
a nonliner function : $y(x, \mathbf{w})$; a liner model of w
error function
$$ \begin{equation} E(\mathbf{w})=\frac{1}{2} \sum_{n=1}^{N}\left\{y\left(x_{n}, \mathbf{w}\right)-t_{n}\right\}^2 \end{equation} $$ Error function > 0
fitting Result
root mean square(RMS)
\begin{equation} E_{\mathrm{RMS}}=\sqrt{2 E\left(\mathbf{w}^{\star}\right) / N} \end{equation}
Over-fitting
increase datasize
regularization
adding a penalty term
Probability Theory
sum rule and product rule
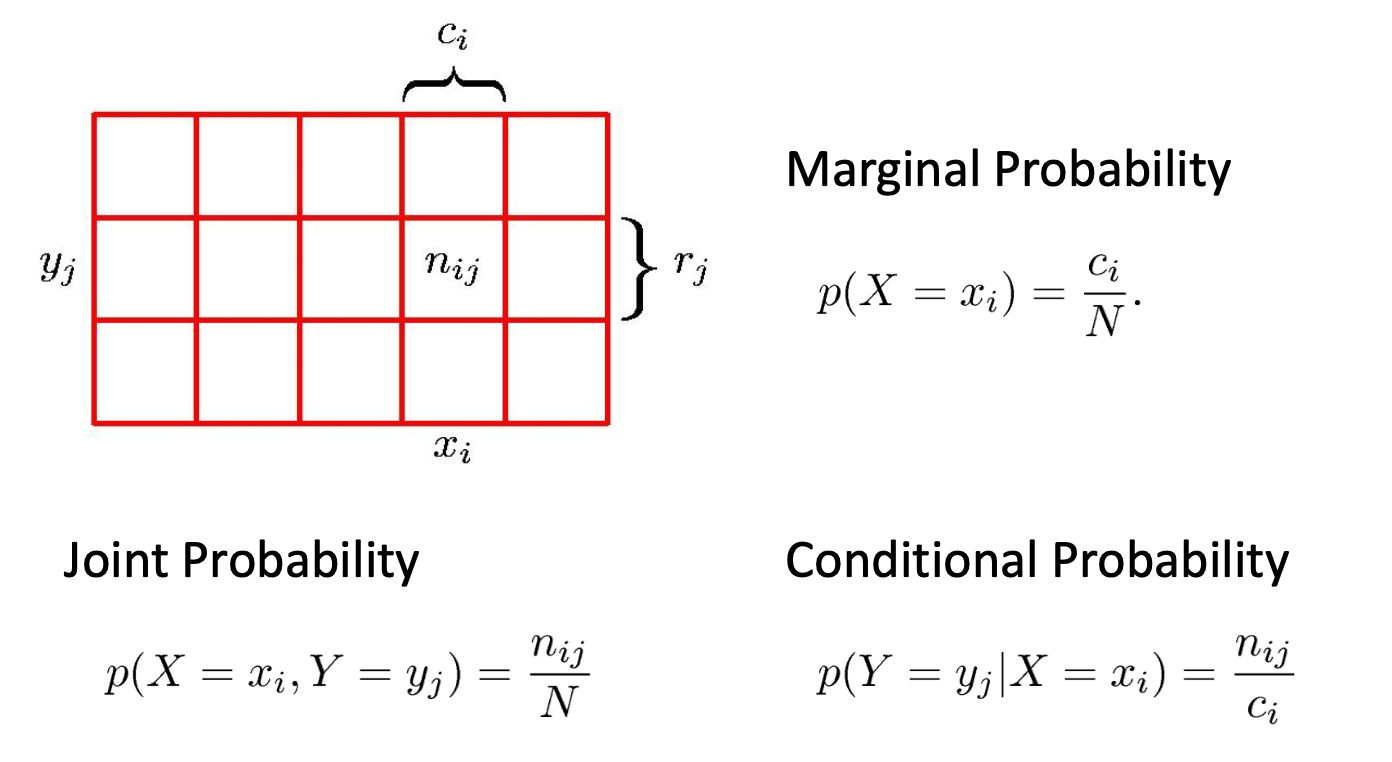
- SUM RULE: $p(X) = \sum_Y p(X,Y)$
- PRODUCT RULE: $p(X,Y) = p(Y|X)p(X)$
Bayes theorem
product theorem twice
expectation and condition expectation
expectation
conditional expectation
variance
covariance
Bayesian probabilities: probabilities provide a quantification of uncertainty
what is Bayes viewpoint, still a mystery https://cyx0706.github.io/2020/10/24/deep-learning-intro/

