TB_SlaterKoster

TB reference

Slater Koster term (from Wiki )

In 1954 J.C. Slater and G.F. Koster published, mainly for the calculation of transition metal d-bands, a table of interatomic matrix elements¹

$E_{i, j}\left(\overrightarrow{\mathbf{r}}_{n, n^{\prime}}\right)=\left\langle n, i|H| n^{\prime}, j\right\rangle$

which can also be derived from the cubic harmonic orbitals straightforwardly. The table expresses the matrix elements as functions of LCAO two-centre bond integrals between two cubic harmonic orbitals, i and j, on adjacent atoms. The bond integrals are for example the $V_{s s \sigma}, V_{p p \pi}$ and $V_{d d \delta}$ for sigma, pi and delta bonds (Notice that these integrals should also depend on the distance between the atoms, i.e. are a function of (l,m,n), even though it is not explicitly stated every time.).

The interatomic vector is expressed as $\overrightarrow{\mathbf{r}}_{n, n^{\prime}}=\left(r_{x}, r_{y}, r_{z}\right)=d(l, m, n)$

where d is the distance between the atoms and l, m and n are the direction cosines to the neighboring atom.

s-p block

$$\begin{aligned} &E_{s, s}=V_{s s \sigma} \newline &E_{s, x}=l V_{s p \sigma} \newline &E_{x, x}=l^{2} V_{p p \sigma}+\left(1-l^{2}\right) V_{p p \pi} \newline &E_{x, y}=l m V_{p p \sigma}-l m V_{p p \pi} \newline &E_{x, z}=\ln V_{p p \sigma}-\ln V_{p p \pi} \end{aligned}$$

s-d block $$ \begin{aligned} &E_{s, x y}=\sqrt{3} l m V_{s d \sigma} \newline &E_{s, x^{2}-y^{2}}=\frac{\sqrt{3}}{2}\left(l^{2}-m^{2}\right) V_{s d \sigma} \newline &E_{s, 3 z^{2}-r^{2}}=\left[n^{2}-\left(l^{2}+m^{2}\right) / 2\right] V_{s d \sigma} \end{aligned} $$

p-d block $$ \begin{aligned} &E_{x, x y}=\sqrt{3} l^{2} m V_{p d \sigma}+m\left(1-2 l^{2}\right) V_{p d \pi} \newline &E_{x, y z}=\sqrt{3} l m n V_{p d \sigma}-2 l m n V_{p d \pi} \newline &E_{x, z x}=\sqrt{3} l^{2} n V_{p d \sigma}+n\left(1-2 l^{2}\right) V_{p d \pi} \newline &E_{x, x^{2}-y^{2}}=\frac{\sqrt{3}}{2} l\left(l^{2}-m^{2}\right) V_{p d \sigma}+l\left(1-l^{2}+m^{2}\right) V_{p d \pi} \newline &E_{y, x^{2}-y^{2}}=\frac{\sqrt{3}}{2} m\left(l^{2}-m^{2}\right) V_{p d \sigma}-m\left(1+l^{2}-m^{2}\right) V_{p d \pi} \newline &E_{z, x^{2}-y^{2}}=\frac{\sqrt{3}}{2} n\left(l^{2}-m^{2}\right) V_{p d \sigma}-n\left(l^{2}-m^{2}\right) V_{p d \pi} \newline &E_{x, 3 z^{2}-r^{2}}=l\left[n^{2}-\left(l^{2}+m^{2}\right) / 2\right] V_{p d \sigma}-\sqrt{3} \ln ^{2} V_{p d \pi} \newline &E_{y, 3 z^{2}-r^{2}}=m\left[n^{2}-\left(l^{2}+m^{2}\right) / 2\right] V_{p d \sigma}-\sqrt{3} m n^{2} V_{p d \pi} \newline &E_{z, 3 z^{2}-r^{2}}=n\left[n^{2}-\left(l^{2}+m^{2}\right) / 2\right] V_{p d \sigma}+\sqrt{3} n\left(l^{2}+m^{2}\right) V_{p d \pi} \end{aligned} $$ d-d block $$ \begin{aligned} &E_{x y, x y}=3 l^{2} m^{2} V_{d d \sigma}+\left(l^{2}+m^{2}-4 l^{2} m^{2}\right) V_{d d \pi}+\left(n^{2}+l^{2} m^{2}\right) V_{d d \delta} \newline &E_{x y, y z}=3 l m^{2} n V_{d d \sigma}+\ln \left(1-4 m^{2}\right) V_{d d \pi}+\ln \left(m^{2}-1\right) V_{d d \delta} \newline &E_{x y, z x}=3 l^{2} m n V_{d d \sigma}+m n\left(1-4 l^{2}\right) V_{d d \pi}+m n\left(l^{2}-1\right) V_{d d \delta} \newline &E_{x y, x^{2}-y^{2}}=\frac{3}{2} l m\left(l^{2}-m^{2}\right) V_{d d \sigma}+2 l m\left(m^{2}-l^{2}\right) V_{d d \pi}+\left[l m\left(l^{2}-m^{2}\right) / 2\right] V_{d d \delta} \newline &E_{y z, x^{2}-y^{2}}=\frac{3}{2} m n\left(l^{2}-m^{2}\right) V_{d d \sigma}-m n\left[1+2\left(l^{2}-m^{2}\right)\right] V_{d d \pi}+m n\left[1+\left(l^{2}-m^{2}\right) / 2\right] V_{d d \delta} \newline &E_{z x, x^{2}-y^{2}}=\frac{3}{2} n l\left(l^{2}-m^{2}\right) V_{d d \sigma}+n l\left[1-2\left(l^{2}-m^{2}\right)\right] V_{d d \pi}-n l\left[1-\left(l^{2}-m^{2}\right) / 2\right] V_{d d \delta} \newline &E_{x y, 3 z^{2}-r^{2}}=\sqrt{3}\left[l m\left(n^{2}-\left(l^{2}+m^{2}\right) / 2\right) V_{d d \sigma}-2 l m n^{2} V_{d d \pi}+\left[l m\left(1+n^{2}\right) / 2\right] V_{d d \delta}\right] \newline &E_{y z, 3 z^{2}-r^{2}}=\sqrt{3}\left[m n\left(n^{2}-\left(l^{2}+m^{2}\right) / 2\right) V_{d d \sigma}+m n\left(l^{2}+m^{2}-n^{2}\right) V_{d d \pi}-\left[m n\left(l^{2}+m^{2}\right) / 2\right] V_{d d \delta}\right] \newline &E_{z x, 3 z^{2}-r^{2}}=\sqrt{3}\left[\ln \left(n^{2}-\left(l^{2}+m^{2}\right) / 2\right) V_{d d \sigma}+\ln \left(l^{2}+m^{2}-n^{2}\right) V_{d d \pi}-\left[\ln \left(l^{2}+m^{2}\right) / 2\right] V_{d d \delta}\right] \newline &E_{x^{2}-y^{2}, x^{2}-y^{2}}=\frac{3}{4}\left(l^{2}-m^{2}\right)^{2} V_{d d \sigma}+\left[l^{2}+m^{2}-\left(l^{2}-m^{2}\right)^{2}\right] V_{d d \pi}+\left[n^{2}+\left(l^{2}-m^{2}\right)^{2} / 4\right] V_{d d \delta} \newline &E_{x^{2}-y^{2}, 3 z^{2}-r^{2}}=\sqrt{3}\left[\left(l^{2}-m^{2}\right)\left[n^{2}-\left(l^{2}+m^{2}\right) / 2\right] V_{d d \sigma} / 2+n^{2}\left(m^{2}-l^{2}\right) V_{d d \pi}+\left[\left(1+n^{2}\right)\left(l^{2}-m^{2}\right) / 4\right] V_{d d \delta}\right] \newline &E_{3 z^{2}-r^{2}, 3 z^{2}-r^{2}}=\left[n^{2}-\left(l^{2}+m^{2}\right) / 2\right]^{2} V_{d d \sigma}+3 n^{2}\left(l^{2}+m^{2}\right) V_{d d \pi}+\frac{3}{4}\left(l^{2}+m^{2}\right)^{2} V_{d d \delta} \end{aligned} $$

Cubic harmonic

The question is how to derive it for easy coding, actually just type them step by step is the best way!

In practice, the coordinate system that is used in such cases is most often a Cartesian coordinate system instead of a spherical coordinate system. In a Cartesian coordinate system the atomic orbitals are often expressed as

$$ \psi_{n l c}(\mathbf{r})=R_{n l}(r) X_{l c}(\mathbf{r}) $$

with the cubic harmonics,²³⁴ $X_{l c}(\mathbf{r})$, as a basis set. LCAO and MO calculations in computational chemistry or tight binding calculations in solid-state physics use cubic harmonics as an atomic orbital basis. The indices lc are denoting some kind of Cartesian representation.

First of all, the cubic harmonics are real functions, while spherical harmonics are complex functions.

The complex numbers are two-dimensional with a real part and an imaginary part. Complex numbers offer very handsome and effective tools to tackle mathematical problems analytically but they are not very effective when they are used for numerical calculations. Skipping the imaginary part saves half the calculational effort in summations, a factor of four in multiplications and often factors of eight or even more when it comes to computations involving matrices.

Table of cubic harmonics

The s-orbitals

The s-orbitals only have a radial part.

$$ \begin{aligned} &\psi_{n 00}(\mathbf{r})=R_{n 0}(r) Y_{0}^{0} \newline &s=X_{00}=Y_{0}^{0}=\frac{1}{\sqrt{4 \pi}} \end{aligned} $$

The p-orbitals

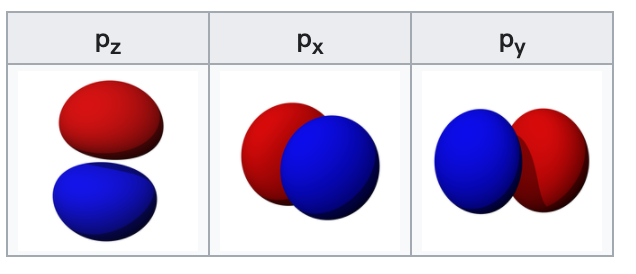
The three p-orbitals are atomic orbitals with an angular momentum quantum number ℓ = 1. The cubic harmonic expression of the p-orbitals

$$ \begin{aligned} p_{z} &=N_{1}^{c} \frac{z}{r}=Y_{1}^{0} \newline p_{x} &=N_{1}^{c} \frac{x}{r}=\frac{1}{\sqrt{2}}\left(Y_{1}^{-1}-Y_{1}^{1}\right) \newline p_{y} &=N_{1}^{c} \frac{y}{r}=\frac{i}{\sqrt{2}}\left(Y_{1}^{-1}+Y_{1}^{1}\right) \end{aligned} $$

with

$$ N_{1}^{c}=\left(\frac{3}{4 \pi}\right)^{1 / 2} $$

The d-orbitals

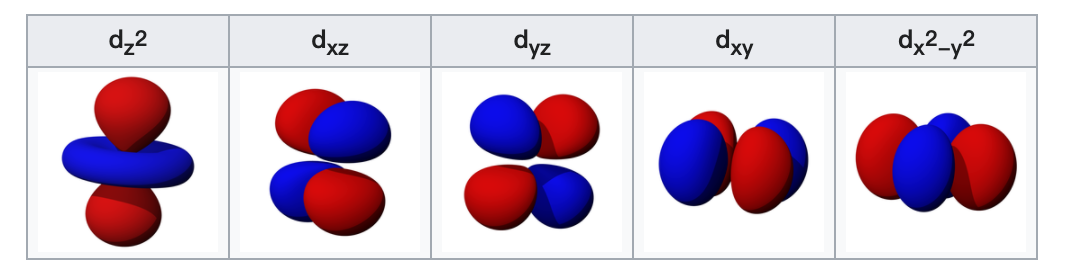
The five d-orbitals are atomic orbitals with an angular momentum quantum number ℓ = 2. The angular part of the d-orbitals are often expressed like

$$ \psi_{n 2 c}(\mathbf{r})=R_{n 2}(r) X_{2 c}(\mathbf{r}) $$ The angular part of the d-orbitals are the cubic harmonics $X_{2 c}(\mathbf{r})$

The f-orbitals

The seven f-orbitals are atomic orbitals with an angular momentum quantum number ℓ = 3. often expressed like

$$ \psi_{n 3 c}(\mathbf{r})=R_{n 3}(r) X_{3 c}(\mathbf{r}) $$ The angular part of the f-orbitals are the cubic harmonics $X_{3 c}(\mathbf{r})$. In many cases different linear combinations of spherical harmonics are chosen to construct a cubic f-orbital basis set.