vasplib:HR HR - a powerful TB tools

HR class 入门

HR - a powerful TB tools

** 什么是 HR? **

In solid-state physics , the tight-binding model (or TB model) is an approach to the calculation of electronic band structure using an approximate set of wave functions based upon superposition of wave functions for isolated atoms located at each atomic site.

$$ \begin{array}{l} H=-t\sum_{\langle i,j\rangle ,\sigma } \left(c_{i,\sigma }^{\dagger } c_{j,\sigma } +h.c.\right)\newline c_{i\sigma }^{\dagger } ,c_{j\sigma } \textrm{-} \textrm{creation}\textrm{and}\textrm{annihilation}\textrm{operators}\newline \sigma \textrm{-}\textrm{spin}\textrm{polarization}\newline t\textrm{-}\textrm{hopping}\textrm{integral}\newline \langle i,j\rangle -\textrm{nearest}\textrm{neighbor}\textrm{index}\newline h.c.\textrm{-}\textrm{the}\textrm{hermitian}\textrm{conjugate}\textrm{of}\textrm{the}\textrm{other}\textrm{term(s)} \end{array} $$

考虑有平移对称性的体系，我们可以只需要考虑元胞与其他晶胞(包括元胞)的相互作用，则可以研究整个体系的物理性质。

以 SSH 模型为例

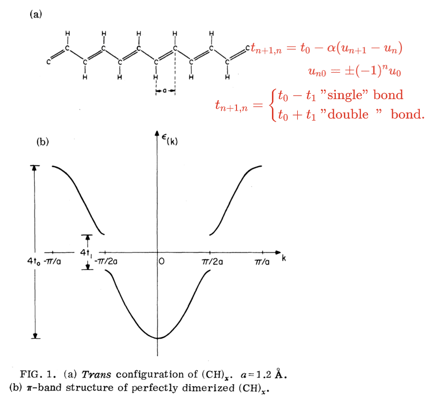
一个元胞里有两个C 元胞内为双键 元胞外为单键，用v 和 w 来代替

上图 有10 个元胞，省空间我们认为只有5个元胞，用哈密顿量用矩阵表示即为

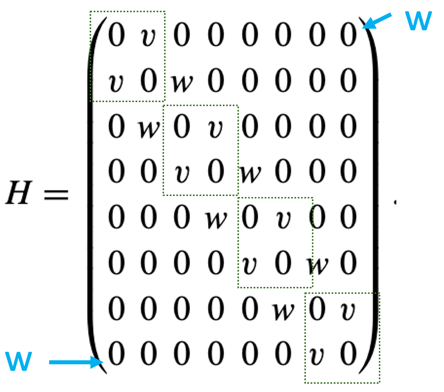
如果加上周期平移条件，即第五个元胞和第一个元胞有相互作用,则需要添上两个蓝色的 元胞间相互作用

这么一个体系可以任意扩写，遵从一定的规律， 即绿框的对角块都是一样的，元胞与元胞之间的Hopping块，依次放在对角块的两边，且满足厄米对称性。

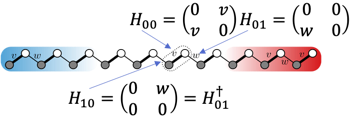
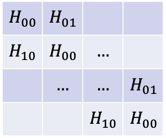
则体系可以用 格点与元胞之间的矩阵所描述，借助于 wannier90: case_hr.dat的输出格式

hr_datformat:

0 0 0 [0 v;v 0]  
1 0 0 [0 0;w 0]   
-1 0 0 [0 w;0 0]  
...

了解了什么是HR后，我们就可以开始我们的HR入门之旅了。

Quickstart

构建一个HR 读取wannier90_hr.dat

1HR_TB = HR.from_wannier90('wannier90_hr.dat')

    vectorL: [185x3 double]
      HnumL: [6x6x185 double]
      HcoeL: [6x6x185 sym]
      NRPTS: 185
    WAN_NUM: 6
   Line_000: 93
  Basis_num: []
         Rm: [3x3 double]
         Gk: [3x3 double]
symvar_list: [1x0 sym]

我们读取了一个 wannier90 生成的一个TB模型

简单看来，这个HR对象 拥有几个基本的属性，vectorL, HnumL, HcoeL, NRPTS, WAN_NUM,Rm,Gk

Bais_num 在这里等效于WAN_NUM,* symvar_list* 先不用管，

• vectorL: 格点的位置HR中的R
• HnumL：R所对应的与元胞的hopping矩阵，数值化的
• HcoeL：HR的一大特点很多方法同时支持符号和数值的哈密顿量，同时设定HcoeL也方便我们后续的操作与调试。在这里读取的是wannier，HcoeL为0
• NRPTS：有多少格点，往往 读取wannier的结果NRPTS比较大 自己做的模型往往只考虑最近邻模型
• WAN_NUM: 元胞中的轨道数量
• Rm: 元胞的基失矩阵
• Gk: 相应的 倒格式矩阵，Gk = 2*pi*(eye(3)/Rm).'

当然可以很快地锁定HOPPING项, 常用的HOMECELL的矩阵

1HR_TB.HnumL(:,:,HR_TB.Line_000)

 1.1466    0.1710         0         0   -0.1335         0  
 0.1710   -1.3207         0         0   -0.2709         0  
     0         0    1.1466    0.1710         0    0.1335  
     0         0    0.1710   -1.3207         0    0.2709  
-0.1335   -0.2709         0         0    4.3787         0  
     0         0    0.1335    0.2709         0    4.3787  

手动构建HR

声明一个空的HR

这里我们手动来定义SSH的

1WAN_NUM = 2;
2HR_TB = HR(WAN_NUM)

    vectorL: [0 0 0]
      HnumL: [2x2 double]
      HcoeL: [2x2 sym]
      NRPTS: 1
    WAN_NUM: 2
   Line_000: 1
  Basis_num: []
         Rm: [3x3 double]
         Gk: [3x3 double]
symvar_list: [1x0 sym]

在没有引入晶格信息之前，HR的默认Rm 为 eye(1)

设置符号化变量

1syms v w real

通过 set_hop 方法来设定 hopping

H_hr = H_hr.set_hop(amp,hi,hj,vector_list,mode)

1 HR_TB = HR_TB.set_hop(v,1,2,[0,0,0],'sym');
2 HR_TB = HR_TB.set_hop(v,2,1,[0,0,0],'sym');
3 HR_TB = HR_TB.set_hop(w,2,1,[1,0,0],'sym');
4 HR_TB = HR_TB.set_hop(w,1,2,[-1,0,0],'sym');

导入POSCAR的信息,（vasplib中大部分的输入输出文件都是仿照VASP的格式） 格式详解见

POSCAR_SSH
1.0
3 0.0000000000 0.0000000000
0 3 0.0000000000
0.0000000000 0.0000000000 20.0000000000
C Si
1 1
Direct
0.25 0.25 0.5
0.75 0.75 0.5

Vesta 中可以看到

1 HR_TB = HR_TB <= 'POSCAR_SSH';

我们也可以用matlab简单看下（TEST）

1HR_TB.show('HOPPING','TwoD',true);

自动构建HR

Slater Koster

之前已经介绍过Slater Koster方法，HR支持自动SlaterKoster型的TB构建.

通过对称性构建

只要写出对称的矩阵表示，就可以构建包含在对称性允许下所有可能项的HR.