陈数计算方法高效法!自旋陈数等sub-band 陈数的计算实例!
陈数计算高效法
中文名称来源于关老师的博客 参考文献-Chern Numbers in Discretized Brillouin Zone: Efficient Method of Computing (Spin) Hall Conductances 1
核心要点在于把二维布里渊区分成很多小份,每一份通过计算贝里联络来计算贝里曲率
Ref.11 把计算要点说的很明确,
- 定义 U(1) link variable: $U_{\mu}\left(k_{\ell}\right) \equiv\left\langle n\left(k_{\ell}\right) \mid n\left(k_{\ell}+\hat{\mu}\right)\right\rangle / \mathcal{N}{\mu}\left(k{\ell}\right)$, where $\mathcal{N}{u}\left(k{\ell}\right) \equiv\left|\left\langle n\left(k_{\ell}\right) \mid n\left(k_{\ell}+\hat{\mu}\right)\right\rangle\right|$
- 定义 lattice field strength $F_{12}$(原通过贝里联络定义$F_{12}(k)=\partial_{1} A_{2}(k)-\partial_{2} A_{1}(k)$, 通过定义我们知道这实质就是贝里曲率,又称Berry Flux,这点不是很确定 随后再说): $\tilde{F}{12}\left(k{\ell}\right) \equiv \ln U_{1}\left(k_{\ell}\right) U_{2}\left(k_{\ell}+\hat{1}\right) U_{1}\left(k_{\ell}+\hat{2}\right)^{-1} U_{2}\left(k_{\ell}\right)^{-1}$
- 最后 $\tilde{\boldsymbol{c}}_{n} \equiv \frac{1}{2 \pi \mathrm{i}} \sum_{\ell} \tilde{\boldsymbol{F}}_{12}\left(k_{\ell}\right)$
核心算法:
1 function BC = BerryCuvature_Discrete_2D(VV,Vk1,Vk2,Vk1k2)
2 % VV W_d_0;
3 % Vk1 W_d_1; 略偏离kx的波函数
4 % Vk2 W_d_2; 略偏离ky的波函数
5 % Vk1k2 W_d_12; 略偏离kx,ky的波函数
6 %
7 % U(1) like variable
8 Uk1 = det(VV'*Vk1);Uk1 = Uk1/norm(Uk1);
9 Uk2 = det(VV'*Vk2);Uk2 = Uk2/norm(Uk2);
10 Uk1_k2 = det(Vk2'*Vk1k2);Uk1_k2 = Uk1_k2/norm(Uk1_k2);
11 Uk2_k1 = det(Vk1'*Vk1k2);Uk2_k1 = Uk2_k1/norm(Uk2_k1);
12 % berry curvature
13 BC = log(Uk1*Uk2_k1/(Uk1_k2*Uk2));
14 BC = imag(BC);
15 BC = sum(BC);
16 end
陈数高效法多带模型
与前文一样,只需要推广 U(1) link variable:
- 推广 U(1) link variable: $U_{\mu}\left(k_{\ell}\right)=\frac{1}{\mathcal{N}{\mu}\left(k{\ell}\right)} \operatorname{det} \psi^{\dagger}\left(k_{\ell}\right) \psi\left(k_{\ell}+\hat{\mu}\right)$ with the normalization constant $\mathcal{N}{\mu}\left(k{\ell}\right) \equiv \mid \operatorname{det} \psi^{\dagger}\left(k_{\ell}\right) \psi\left(k_{\ell}+\hat{\mu}\right)\mid$
direct
所谓高效法似乎添加了一些额外计算,而Topocondmat 总结的方法也非常清楚,后续可以再试
the final recipe to compute the Chern number is as follows: grid up the BZ into small plaquettes labelled by n
$$\Phi_{n}=\operatorname{Arg}\left[\prod_{p} \operatorname{Det}\left[\left\langle u_{s}\left(\mathbf{k}{\mathbf{n}, \mathbf{p}}\right) \mid \mathbf{u}{\mathbf{s}^{\prime}}\left(\mathbf{k}{\mathbf{n}, \mathbf{p}+\mathbf{1}}\right)\right\rangle\right]\right]$$ Compute the flux through each plaquette where $\mathbf{k}{\mathbf{n}, \mathbf{p}}$} are momenta on the corners of the lattice. The Chern number is calculated as $$v=(2 \pi)^{-1} \sum_{n} \Phi_{n}$$
Example
Haldane模型
我们通过 vasplib的Htig类定义Haldane模型
1% Haldane
2syms h theta phi real;
3%
4% phi = 0;
5sigma_0 = [1 0;0 1];
6sigma_x = [0 1;1 0];
7sigma_y = [0 -1i;1i 0];
8sigma_z = [1 0;0 -1];
9%%
10syms a t t_2 M phi delta k_x k_y real;
11%
12%
13Rm = [1 0;-1/2 sqrt(3)/2]*a;
14Haldane= Htrig(2);
15t1 = [1/3,2/3]*a;
16t2 = [2/3,1/3]*a;
17%
18e1 = t1-t2+[0 0]*Rm;
19e2 = t1-t2+[1 0]*Rm;
20e3 = t1-t2+[0 -1]*Rm;
21d1 = [1 0]*Rm;
22d2 = [0 1]*Rm;
23d3 = [-1 -1]*Rm;
24% H12 = -t*(...
25% cos(e1*[k_x;k_y]) +cos(e2*[k_x;k_y])+cos(e3*[k_x;k_y])...
26% - ...
27% 1i*sin(e1*[k_x;k_y]) +sin(e2*[k_x;k_y])+cos(e3*[k_x;k_y]));
28%
29% H21 = conj(H12);
30H12trig_r = Trig(-t*(cos(e1*[k_x;k_y]) +cos(e2*[k_x;k_y])+cos(e3*[k_x;k_y])),sigma_x);
31H12trig_i = Trig(-t*(sin(e1*[k_x;k_y]) +sin(e2*[k_x;k_y])+sin(e3*[k_x;k_y])),sigma_y);
32H11_0 = Trig(-2*t_2*cos(phi)*(cos(d1*[k_x;k_y]) +cos(d2*[k_x;k_y])+cos(d3*[k_x;k_y])),sigma_0);
33H11_z = Trig((M-2*t_2*sin(phi))*(sin(d1*[k_x;k_y]) +sin(d2*[k_x;k_y])+sin(d3*[k_x;k_y])),sigma_z);
34a = 1;
35%
36Haldane= Haldane+ H12trig_r + H12trig_i+ H11_0+ H11_z;
37Haldane.Rm = double(subs(Rm));
38disp(Haldane);
Haldane 模型的体能带
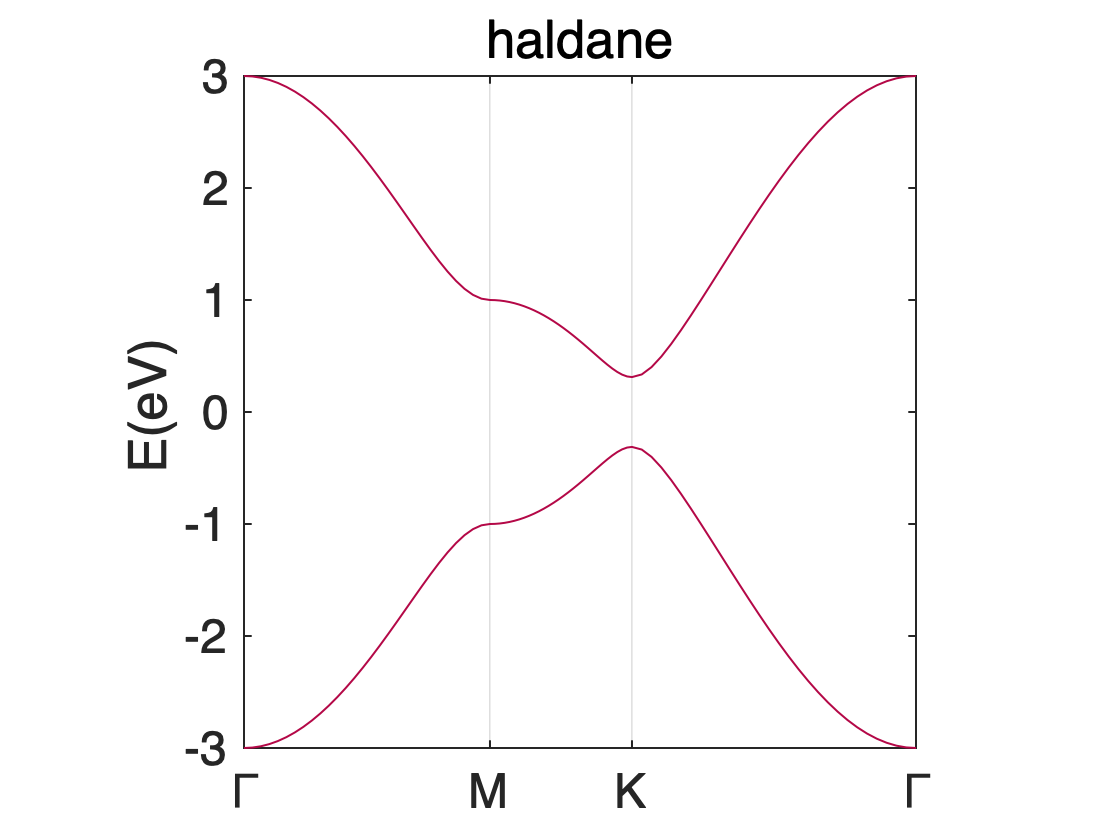
BerryCurvature

对BC求和: 陈数等于 -6.283185307179586/$2\pi$ = -1
Individual Chern numbers3
In general, if the Hilbert space H of a given problem can be written as a sum of smooth Hilbert spaces, $$ \mathscr{H}=\bigoplus_{i} \mathscr{H}_{i} $$ then each of the Hilbert spaces has a well-defined Chern number $C_i$. These individual Chern numbers sum together to the Chern number of the full Hilbert space: $$C = \sum_i C_i$$
In the presence of a symmetry S however, the Hilbert space can be split up according to the symmetry eigenvalues. For example, consider a mirror symmetry with eigenvalues $\pm i$. On the mirror-symmetric surface, S and H(k) commute. Therefore, the Bloch functions $|u_{n,k}⟩$ can be separated into +i and −i eigenstates. Both eigenspaces have a well- defined Chern number: $C = C_i +C_{−i}$. This gives rise to a symmetry-protected topological classification. Materials can have a zero total Chern number, but non-zero individual Chern numbers. Such a topological phase is protected as long as both the band gap remains open and the symmetry is respected. If the symmetry is broken, a mixing of the two eigenspaces can change the topological phase.
Spin Chern Number
Time-reversal symmetry $\mathcal{T}$ leads to a particularly interesting and well-known topological classification. It is an anti-unitary symmetry and squares to −1($\mathcal{T}^2 = -1$) in the spinful case. As a result, the Bloch functions come in so-called Kramers pairs:
$$\begin{aligned}\mathcal{T}\left|u_{m, \mathbf{k}}^{I}\right\rangle &=\left|u_{m, \mathbf{k}}^{I I}\right\rangle \\ \mathcal{T}\left|u_{m, \mathbf{k}}^{I I}\right\rangle &=-\left|u_{m, \mathbf{k}}^{I}\right\rangle \end{aligned}$$
The two groups then have individual Chern numbers $C_I$ and $C_II$. It should be noticed these chern numbers are not Gauge-invariant. Therefore, a topological invariant $Z_2$ can be defined as $C_I$ mod 2.
BHZ 2D
定义 BHZ k·p 模型
1%% useful tool
2s_0 = pauli_matric(0) ; s_x = pauli_matric(1); s_y = pauli_matric(2) ; s_z = pauli_matric(3);
3sigma_0 = pauli_matric(0);sigma_x = pauli_matric(1);sigma_y = pauli_matric(2);sigma_z = pauli_matric(3);
4tau_0 = pauli_matric(0); tau_x = pauli_matric(1); tau_y = pauli_matric(2); tau_z = pauli_matric(3);
5%k·p model
6syms C0 C1 C2 real;
7syms M0 M1 M2 real;
8syms A B1 B2 real;
9syms k_x k_y k_z real;
10%
11M = M0-M2*(k_x^2+k_y^2);
12E0k = C0+C2*(k_x^2+k_y^2);
13k_plus = k_x + 1i* k_y;
14k_minus = k_x - 1i* k_y;
15%
16BHZ = HK(4,2)
17%
18BHZ = BHZ ...
19 +Term(A*k_x ,sigma_z*tau_x )...
20 +Term(A*k_y ,sigma_0*tau_y )...
21 +Term(E0k ,sigma_0*tau_0 )...
22 +Term(M ,sigma_0*tau_z )...
23 ;
$$\begin{array}{l} H = \left(\begin{array}{cccc} \sigma_2 & A{\left(-k_y \mathrm{i}+k_x \right)} & 0 & 0\newline A{\left(k_y \mathrm{i}+k_x \right)} & \sigma_1 & 0 & 0\newline 0 & 0 & \sigma_2 & -A{\left(k_y \mathrm{i}+k_x \right)}\newline 0 & 0 & -A{\left(-k_y \mathrm{i}+k_x \right)} & \sigma_1 \end{array}\right)\newline \mathrm{}\newline \textrm{where}\newline \mathrm{}\newline \sigma_1 =C_0 -M_0 +{k_x }^2 {\left(M_2 +C_2 \right)}+{k_y }^2 {\left(M_2 +C_2 \right)}\newline \mathrm{}\newline \sigma_2 =C_0 +M_0 +{k_x }^2 {\left(-M_2 +C_2 \right)}+{k_y }^2 {\left(-M_2 +C_2 \right)} \end{array}$$
时间反演算符定义为 $\mathcal{T} = -i\sigma_y\tau_0\mathbf{\mathcal{K}}$,
即 spinup 和 spindn 的本征值差了一个负号
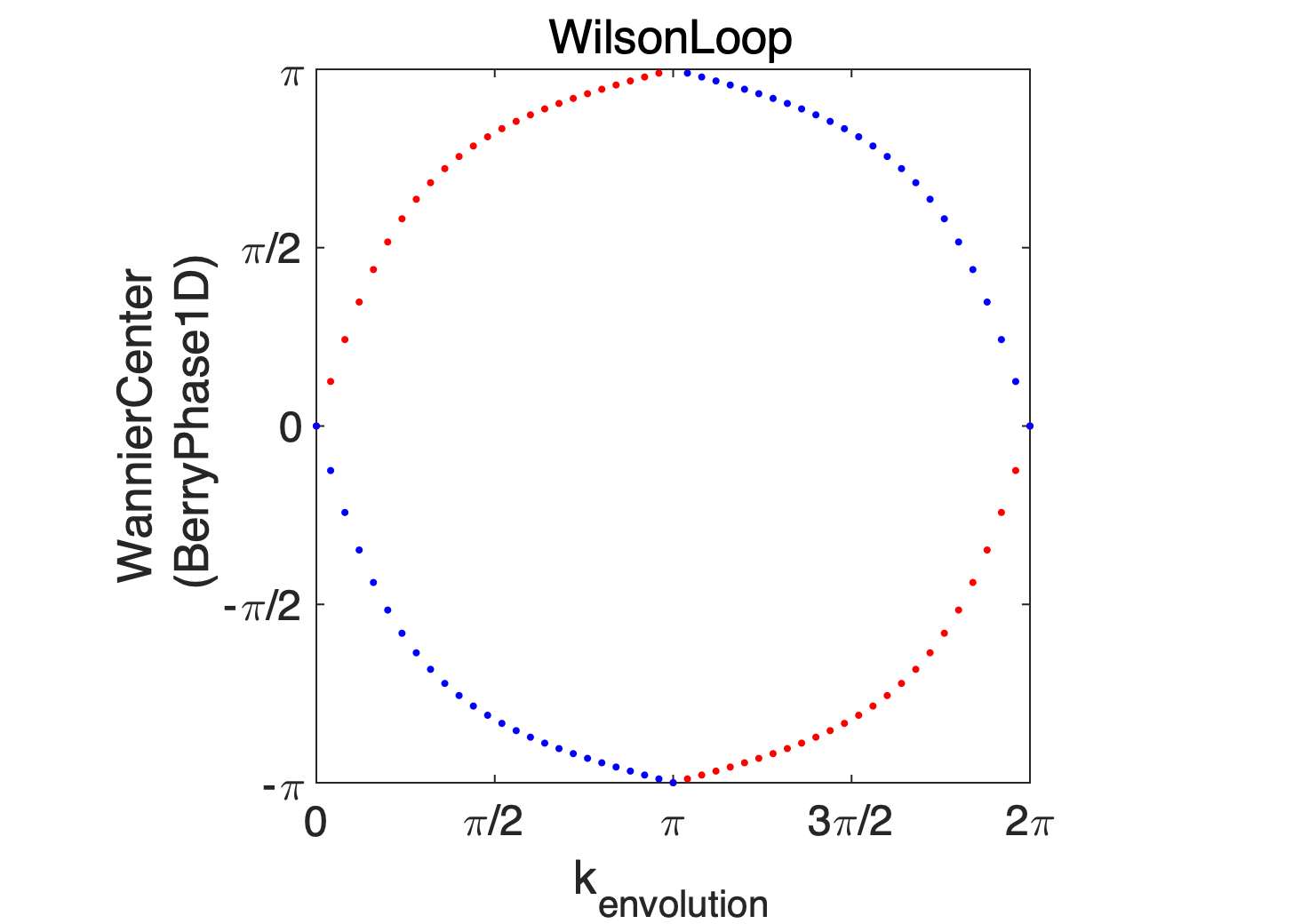
Mirror Chern Number4
$$ H(k)=\left(v_{x} k_{x} \sigma_{x}-v_{y} k_{y} \sigma_{y}\right) \tau_{x}+m \tau_{z} $$ where $\sigma_i$ is the Pauli matrix of spins and $\tau_i$ is that of pseudospins representing two Dirac cones existing in the bulk TCI. $$\left(\begin{array}{cccc} m & 0 & 0 & -k_y ,v_2 ,\mathrm{i}+k_x ,v_1 \newline 0 & -m & -k_y ,v_2 ,\mathrm{i}+k_x ,v_1 & 0\newline 0 & k_y ,v_2 ,\mathrm{i}+k_x ,v_1 & m & 0\newline k_y ,v_2 ,\mathrm{i}+k_x ,v_1 & 0 & 0 & -m \end{array}\right)$$ 可以看到此时 哈密顿量并未写成块直和的形式 这时我们已知 $\mathcal{M}_z = −i\sigma_z\tau_z$. $$\left(\begin{array}{cccc} -\mathrm{i} & 0 & 0 & 0\newline 0 & \mathrm{i} & 0 & 0\newline 0 & 0 & \mathrm{i} & 0\newline 0 & 0 & 0 & -\mathrm{i} \end{array}\right)$$ 这暗示着我们 2,3 orbitals的本征值为i 1,4 orbitals的本征值为-i
Fukui, T., Hatsugai, Y. & Suzuki, H. Chern Numbers in Discretized Brillouin Zone: Efficient Method of Computing (Spin) Hall Conductances. J. Phys. Soc. Jpn. 74, 1674–1677 (2005). ↩︎ ↩︎
Liu, J. et al. Spin-filtered edge states with an electrically tunable gap in a two-dimensional topological crystalline insulator. Nature Mater 13, 178–183 (2014). ↩︎
Soluyanov, A. A. & Vanderbilt, D. Wannier representation of Z 2 topological insulators. Phys. Rev. B 83, 035108 (2011). ↩︎
Hsieh, T. H. et al. Topological crystalline insulators in the SnTe material class. Nature Communications 3, 982 (2012). The effective Hamiltonian for a TCI thin film is given by a two-dimensional model 2, ↩︎

