拓扑电路入门学习

本文打算Follow武汉大学余睿老师的综述 电路中的拓扑态 , 以及他的讲座 在电路中设计新拓扑物态 一些关键的概念需要掌握: 线性电子线路 电路理论(电势运动方程，拉普拉斯矩阵方程) 基尔霍夫方程与TB模型的对应(Onsite energy, hopping, SOC)，基尔霍夫方程的求解, 具体Hspice的模拟我们另开新帖。

概念的阐释

线性电路

线性电路是指完全由线性元件、独立源或线性受控源构成的电路。(来自百度百科 )

Linear circuit : an electronic circuit which obeys the superposition principle(for all linear systems, the net response caused by two or more stimuli is the sum of the responses that would have been caused by each stimulus individually.) $$F\left(a x_1+b x_2\right)=a F\left(x_1\right)+b F\left(x_2\right)$$

线性元件

• ideal resistors
• ideal capacitors
• ideal inductors
• op-amps(operational amplifier)

非线性元件

线性电路的组成单元为线性元件(An element is linear if and only if the terminal voltage v and terminal current i, together with the initial condition, if any, satisfy the homogeneity and additivity properties in the equation that defines the element,就是元件满足线性欧姆定律):

• diodes
• transistors
• iron core inductors
• transformers when the core is saturated.

常见线性电路

• 放大电路
• 积分电路
• 差分电路
• 滤波器

电势运动方程

并没有明确告诉我们电势运动方程是什么，猜测是以基尔霍夫电势方程为基石的运动方程 The fundamental assumption of circuit theory is that the voltages satisfy Kirchhoff’s voltage law (KVL) and the currents satisfy Kirchhoff’s current law (KCL).

• KVL
• KCL

拉普拉斯矩阵方程

基尔霍夫方程与TB模型的对应¹

a little example

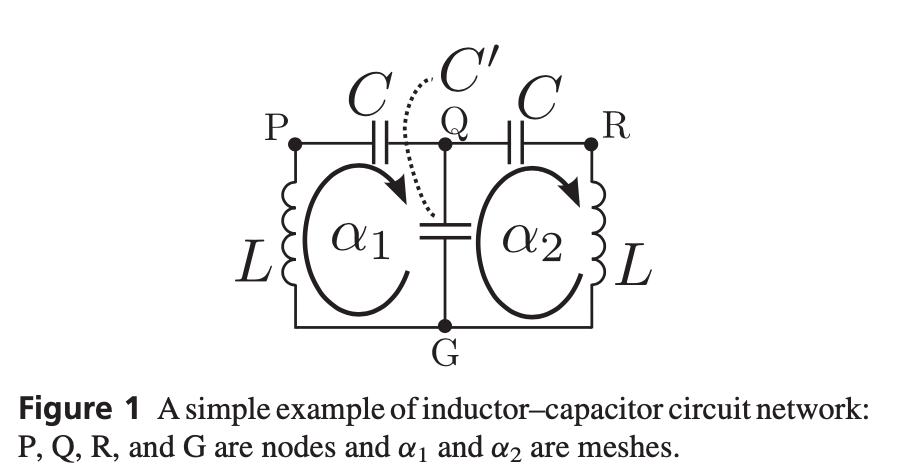
mesh current method

Complex currents $\tilde{J}_1$ and $\tilde{J}_2$ circulate along the two directed meshes $\alpha_1$ and $\alpha_2$. $\tilde{V}_1$ (Q and G)and $\tilde{V}_2$

Hereby: We can represent them by the vector $\tilde{\boldsymbol{J}}=\left[\tilde{J}_1,\tilde{J}_2\right]^{T}$. The voltage drops along $\alpha_1, \alpha_2$ are denoted by $\tilde{\boldsymbol{V}}=\left[\tilde{V}_1,\tilde{V}_2\right]^{T}$. The voltage drop vector $\tilde{\boldsymbol{V}}$ and the mesh current vector $\tilde{J}$ are related as $\tilde{\boldsymbol{V}}=Z(\omega) \tilde{\boldsymbol{J}}$

$$ Z(\omega)=\left[\begin{array}{cc} \mathrm{j} \omega L+1 /\left(\mathrm{j} \omega C_{\mathrm{t}}\right) & -1 /\left(\mathrm{j} \omega C^{\prime}\right) \newline -1 /\left(\mathrm{j} \omega C^{\prime}\right) & \mathrm{j} \omega L+1 /\left(\mathrm{j} \omega C_{\mathrm{t}}\right) \end{array}\right] $$

Due to the KVL, $\tilde{\boldsymbol{V}}$ must be zero, We have $detZ(\omega) = 0$

electrical node potentials

$$ Y(\omega)=\left[\begin{array}{ccc} \mathrm{j} \omega C+1 /(\mathrm{j} \omega L) & -\mathrm{j} \omega C & 0 \newline -\mathrm{j} \omega C & 2 \mathrm{j} \omega C+\mathrm{j} \omega C^{\prime} & -\mathrm{j} \omega C \newline 0 & -\mathrm{j} \omega C & \mathrm{j} \omega C+1 /(\mathrm{j} \omega L) \end{array}\right] $$

MNA

General analysis

the resonance condition and show the analogy between electrical circuits and quantum tight-binding models in solid-state physics.

Resonant circuits with inductances

Resonant circuits with mutual inductances

For this circuit network, $$ \begin{aligned} \hat{Z}(\omega)=& \sum_{i}\left(\mathrm{j} \omega L_{i}+\frac{1}{\mathrm{j} \omega C}\right)\left|\alpha_{i}\right\rangle\left\langle\alpha_{i}\right| \newline &+\mathrm{j} \omega \sum_{i} \sum_{i \neq i} M_{i j}\left|\alpha_{i}\right\rangle\left\langle\alpha_{j}\right| \end{aligned} $$

then $j\omega C\hat{Z}|\Psi\rangle> = 0$

$$ \begin{aligned} j\omega C \hat{Z}(\omega)=& \sum_{i}\left( \xi_{i} \mathrm{j}^2 (\omega/\omega_0)^2 +1\right)\left|\alpha_{i}\right\rangle\left\langle\alpha_{i}\right| \newline &+\mathrm{j}^2 \omega^2 C \sum_{i} \sum_{i \neq i} M_{i j}\left|\alpha_{i}\right\rangle\left\langle\alpha_{j}\right| \end{aligned} $$

then $(\frac{\omega_0}{\omega j})^2j\omega C\hat{Z}|\Psi\rangle = 0$

$$ \begin{aligned} (\frac{\omega_0}{\omega j})^2 j\omega C \hat{Z}(\omega)=& \sum_{i}\left( \xi_{i} +(\frac{\omega_0}{\omega})^2\right)\left|\alpha_{i}\right\rangle\left\langle\alpha_{i}\right| \newline &+ \sout{(\omega^2/\omega_0^2)}/L \sum_{i} \sum_{i \neq i} M_{i j}\left|\alpha_{i}\right\rangle\left\langle\alpha_{j}\right| \end{aligned} $$

We have

$$ \begin{aligned} &\hat{K}|\Psi\rangle=\left(\frac{\omega_{0}}{\omega}\right)^{2}|\Psi\rangle \newline &\hat{K}=\sum_{i} \xi_{i}|\alpha_{i}\rangle\langle\alpha_{i}|-\sum_{i} \sum_{j \neq i} \kappa_{i j}| \alpha_{i}\rangle\langle\alpha_{j}| \end{aligned} $$

where $\omega_0 = 1/\sqrt{LC}$, $\xi_{i}=L_i/L$ and $\kappa_{ij} = - M_{ij}/L$

Then $\hat{K}$ can be interpreted as a Hamiltonian: $$\hat{K}|\Psi\rangle= = \hat{H}|\Psi\rangle = E|\Psi\rangle=\left(\frac{\omega_{0}}{\omega}\right)^{2}|\Psi\rangle$$

Resonant circuits with coupling inductances

We now consider resonant circuits, composed of an inductance Li and a capacitance C connected in parallel to $\pi$i, as shown in Fig. 2(b). $$ \begin{aligned} \hat{Y}(\omega)=& \sum_{i}\left(\frac{1}{j \omega L_{i}}+\mathrm{j} \omega C\right)\left|\pi_{i}\right\rangle\left\langle\pi_{i}\right| \newline &+\sum_{i} \sum_{j \omega L_{i j}}\frac{1}{j \omega L_{ij}}\left(\left|\pi_{i}\right\rangle\left\langle\pi_{i}|-| \pi_{i}\right\rangle\left\langle\pi_{j}\right|\right) \end{aligned} $$

Introducing an inductance L for nondimensionalization, we rewrite the equation $(\frac{\omega_0}{\omega j})^2j\omega L\hat{Y}|\Psi\rangle = 0$ as follows: $$ \hat{K}|\Psi\rangle=\left(\frac{\omega}{\omega_0}\right)^{2}|\Psi\rangle $$

1-D example

1-D Resonant circuits with mutual inductances

$$ \hat{Z}(\omega)=\left(j \omega L+\frac{1}{j \omega C}\right) \hat{1}+j \omega M \sum_{i \in \mathbb{Z}}\left(\left|\alpha_{i-1}\right\rangle\left\langle\alpha_{i}|+| \alpha_{i+1}\right\rangle\left\langle\alpha_{i}\right|\right) $$

Here, we construct $\hat{K}^{(\mathrm{p})}=\sum_{i} \xi_{0}\left|\alpha_{i}\right\rangle\left\langle\alpha_{0}\right|$, $\xi_0= 1$, $\hat{K}^{(\mathrm{h})}=-\sum_{i} \sum_{j \neq i} \kappa \left|\alpha_{i}\right\rangle\left\langle\alpha_{j}\right|$

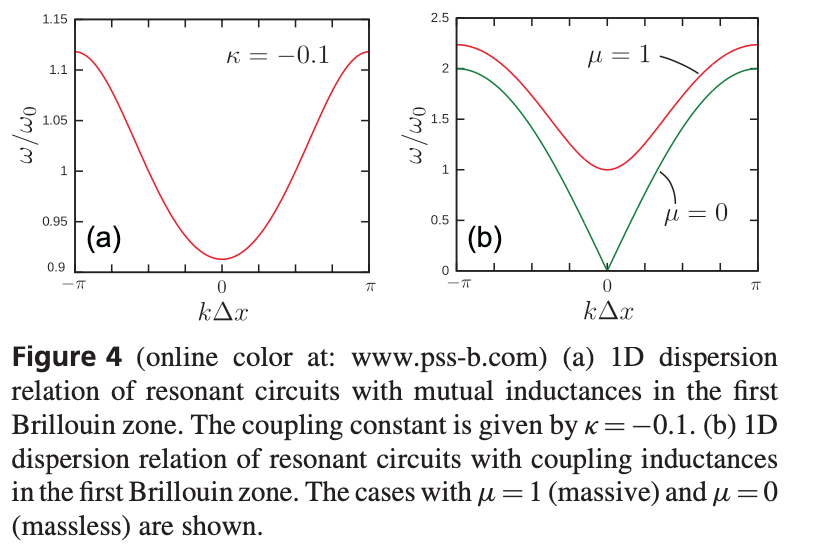
$$H(k) =\xi_{0} + e^{ik\Delta x}\kappa + e^{-ik\Delta x}\kappa$$

$$H(k) = \xi_{0}+ 2cos(k\Delta x)\kappa = (\frac{\omega_{0}}{\omega})^2$$

Resonant circuits with capacitance

对电路网络中的节点进行编号 $\alpha = 1, 2, · · · , N $, 任意两节点 a 和 b 间导纳记为$y_\alpha\beta$. 节点a上的电势记为$v_\alpha$(取地面为零势能参考点), 流入该节点的净电流记为 $I_\alpha$. 对节点$\alpha$ , 从与之相连的节点$\alpha^{\prime}$流入的电流记为$I_\alpha\alpha^{\prime}$, 欧姆定律要求 $I_\alpha\alpha^{\prime} = (v_\alpha^{\prime} - v_\alpha) y_\alpha\alpha^{\prime} $, 求和

$$\sum_{\alpha^{\prime}}(v_\alpha^{\prime} - v_\alpha) y_\alpha\alpha^{\prime} = I_\alpha $$

即 $\mathcal{L} V = I $。

这个时候我们把hopping项换成电容， 利用 孤立的 LC 谐振回路具有特定的谐振频率 $\omega_0$ = $1/\sqrt{LC}$

The admittance matrix Use $Y(\omega)$, 导纳 WaveVector-> Voltage

$$ \begin{aligned} \hat{Y}(\omega)=& \sum_{i}\left(\frac{1}{j \omega L_{i}}+\mathrm{j} \omega C\right)\left|\pi_{i}\right\rangle\left\langle\pi_{i}\right| + \sum_{i} \sum_{j \omega C_{i j}}j\omega C_{ij}\left(\left|\pi_{i}\right\rangle\left\langle\pi_{i}|-| \pi_{i}\right\rangle\left\langle\pi_{j}\right|\right) \end{aligned} $$

$$ \begin{equation} \begin{aligned} \frac{1}{j\omega C}\hat{Y}(\omega)=& \sum_{i}\left(-\frac{\omega_0^2}{ \omega^2 }+ c_i\right)\left|\pi_{i}\right\rangle\left\langle\pi_{i}\right| + \sum_{i} \sum_{c_{ij}}c_{ij}\left(\left|\pi_{i}\right\rangle\left\langle\pi_{i}|-| \pi_{i}\right\rangle\left\langle\pi_{j}\right|\right) \end{aligned} \end{equation} $$

$$ \begin{aligned} \frac{1}{j\omega}\hat{Y}(\omega)=& \sum_{i}\left(-\frac{1}{ \omega^2 L }+ C_i\right)\left|\pi_{i}\right\rangle\left\langle\pi_{i}\right| + \sum_{i} \sum_{C_{ij}}C_{ij}\left(\left|\pi_{i}\right\rangle\left\langle\pi_{i}|-| \pi_{i}\right\rangle\left\langle\pi_{j}\right|\right) \end{aligned} $$

$$ \begin{equation} \begin{aligned} &Y V=\frac{1}{\omega^{2} L} \boldsymbol{V}, \newline &Y=\left[\begin{array}{cccc} y_{1} & -C_{12} & \cdots & -C_{1 N} \newline -C_{21} & y_{2} & \cdots & -C_{2 N} \newline \vdots & \vdots & \ddots & \vdots \newline -C_{N 1} & -C_{N 2} & \cdots & y_{N} \end{array}\right] \newline &y_{\alpha}=\sum_{\alpha^{\prime}=1(\neq \alpha)}^{N} C_{\alpha \alpha^{\prime}}+C_{\alpha} \end{aligned} \end{equation} $$

impedance matrix Use $Z(\omega)$, 阻抗 WaveVector-> Current

For this circuit network, $$ \begin{aligned} \hat{Z}(\omega)=& \sum_{i}\left(\mathrm{j} \omega L+\frac{1}{\mathrm{j} \omega C_{i}}\right)\left|\alpha_{i}\right\rangle\left\langle\alpha_{i}\right|+\frac{1}{\mathrm{j} \omega} \sum_{i} \sum_{i \neq i} \frac{1}{C_{i j}}\left|\alpha_{i}\right\rangle\left\langle\alpha_{j}\right| \end{aligned} $$

$$ \begin{aligned} \frac{1}{\mathrm{j} \omega L}\hat{Z}(\omega)= & \sum_{i}\left(1-\frac{\omega_0^2}{\omega^2 \epsilon_{i}}\right)\left|\alpha_{i}\right\rangle\left\langle\alpha_{i}\right|-\sum_{i} \sum_{i \neq i} \frac{\omega_0^2}{\omega^2\epsilon_{i j}}\left|\alpha_{i}\right\rangle\left\langle\alpha_{j}\right| \end{aligned} $$

$$ \begin{aligned} -(\frac{\omega}{\omega_0})^2\frac{1}{\mathrm{j} \omega L}\hat{Z}(\omega)= & \sum_{i}\left(-(\frac{\omega}{\omega_0})^2+ \frac{1}{\epsilon_{i}}\right)\left|\alpha_{i}\right\rangle\left\langle\alpha_{i}\right|+\sum_{i} \sum_{i \neq i} \frac{1}{\epsilon_{i j}}\left|\alpha_{i}\right\rangle\left\langle\alpha_{j}\right| \end{aligned} $$

所以我们有 $\hat{H}_{circu}\bf{V} =(\frac{\omega}{\omega_0})^2\bf{V}$

$$ \hat{H}_{circu} = \sum_{i} \frac{1}{\epsilon_{i}}|\alpha_{i}\rangle\langle\alpha_{i}| +\sum_{i} \sum_{j \neq i} \frac{1}{\epsilon_{ij}}|\alpha_{i}\rangle\langle\alpha_{j}| $$

拓扑电路领域的关键发展